12/09/2019

Em artigo, Imbuzeiro aborda as impossibilidades matemáticas

Reprodução
do blog do IMPA Ciência & Matemática, de O Globo, coordenado por Claudio Landim

12/09/2019
Roberto Imbuzeiro Oliveira – Pesquisador titular do IMPA

I. Um passatempo que faz muito tempo passar

Proponho um jogo de paciência. Começa com quadrados em branco dispostos em cinco colunas, como na figura 1 abaixo. De início, esses quadrados estão vazios. Ao longo do jogo, você preencherá alguns desses quadrados com um X, e estes passarão a ser chamados de marcados.

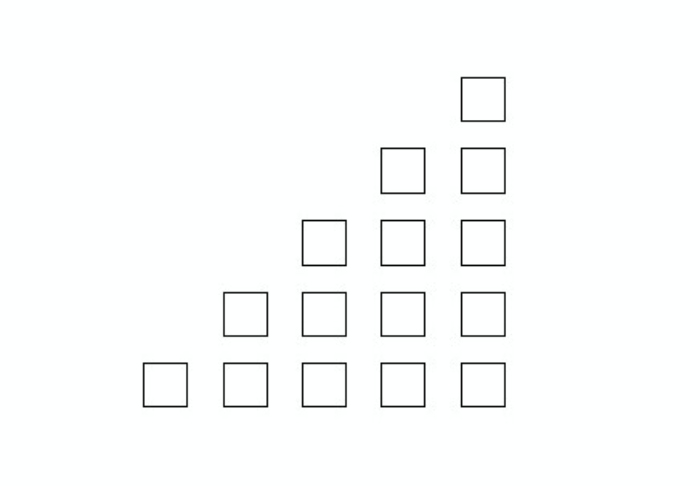
Figura 1: Os quadrados do jogo. Repare que há cinco colunas, contendo 1,2,3,4 e 5 quadradinhos.

Em cada rodada, você deve escolher duas colunas e marcar quadrados vazios nas duas colunas, sempre em igual número. Por exemplo, se uma coluna tem dois quadrados vazios e outra tem quatro, então você pode marcar um ou dois quadrados vazios em cada uma dessas duas colunas. As figuras abaixo ilustram o que pode acontece nas duas primeiras jogadas.

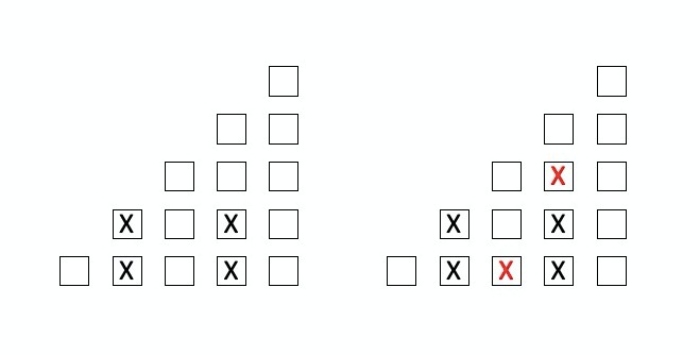
Figura 2: Uma sucessão de jogadas. Na primeira, foram marcados dois X nas colunas 2 e 4 (da esquerda para a direita). Na segunda jogada, marcamos um quadrado vazio em cada uma das colunas 3 e 4.

O jogo termina ou quando todos os quadrados estão marcados ou quando só houver uma coluna ainda com quadrados vazios. Você ganha se todos os quadrados forem marcados e perde em caso contrário. Espero que se arrisque a jogar este jogo e se empenhe para ganhar antes de seguir a leitura.

Conheci este jogo (ou melhor, uma variante dele) no livro Iniciação a Matemática: um curso com problemas e soluções, dos professores Krerley Oliveira (da Universidade Federal de Alagoas) e Adán Corcho (da Universidade Federal do Rio de Janeiro), editado pela Sociedade Brasileira de Matemática. É um ótimo passatempo, na melhor acepção da palavra. Digo isso pelo seguinte: pode passar o tempo que for; você pode tentar quantas vezes quiser, que ainda assim não vai conseguir vencer. É matematicamente impossível ganhar o jogo!

II. O drama da impossibilidade

“Mas pra quem tem pensamento forte
O impossível é só questão de opinião”

Da música “Só os loucos sabem”,

do Charlie Brown Jr.

(composta por A.M. Abrão/T. R. Castanho)

Pensar que algumas coisas são impossíveis pode ser meio desanimador. Por exemplo, se um parente seu está desenganado pelos médicos, pode ser alentador ouvir que “nada é impossível”. A diferença entre este caso e o jogo acima é que a Medicina não é exata: sempre há espaço para o inesperado ou até para um milagre. Já a Matemática é diferente. Alguns teólogos, como São Tomás de Aquino, entendem que Deus não desobedece as leis da Lógica. Se isso é verdade, nem Ele ganharia o jogo acima.

No caso de Deus, falar do impossível rende debates complexos sobre a Sua onipotência – a veja o artigo Omnipotence paradox, da Wikipedia em inglês, para mais detalhes. Na nossa vida comum, o problema de falar “isso é impossível” é outro bem diferente. Se penso que um objetivo é inatingível, posso desistir dele sem razão ou parar de lutar antes da hora. Talvez os visionários, os atletas de elite, os grandes artistas e os caras que se apaixonaram por meninas muito mais bonitas do que eles devam mesmo pensar que “o impossível é só questão de opinião” (deu certo comigo!).

Ao mesmo tempo, se há coisas mesmo impossíveis, não seria melhor saber logo? Imagine, por exemplo, que eu me obstino no jogo. Eu poderia tentar de novo e de novo, imaginando que das vezes anteriores me faltou inteligência, experiência ou atenção. Com isso, sofreria desnecessariamente.

Agora imagine outra situação, em que o jogo é uma tarefa do meu trabalho. Meu chefe é taxativo.

— Continue tentando até conseguir!

Eu poderia responder “Mas, chefe, esse jogo é impossível!”. No entanto se eu não desse uma prova de que não dá para ganhar, ele não teria porque acreditar em mim. Ele poderia até me chamar de “burro”! Para botar mais lenha na fogueira, ele poderia dizer que conseguiu ganhar com um número maior de quadrados a serem preenchidos, como na figura 3 abaixo. Se com mais é possível, por que não seria com menos?

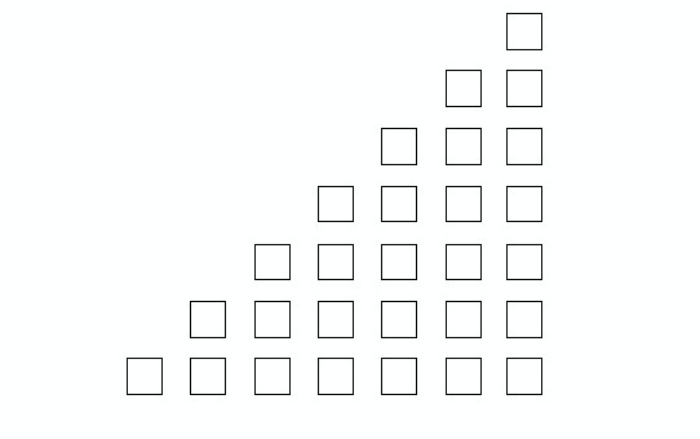
Figura 3: O jogo começa com 7 colunas, preenchidas com 1,2,3,4,5,6 e 7 quadrados. Neste caso, é possível ganhar o jogo. Você consegue descobrir como?

Neste caso, meu problema não é psicológico e sim lógico. Preciso demonstrar a Deus e ao mundo que a tarefa realmente é impossível.

III. O impossível na história da Matemática

Todos conhecemos teoremas como o de Pitágoras, que nos permitem fazer ou calcular alguma coisa. Há, no entanto, uma série de resultados matemáticos que se parecem com o meu problema acima: eles falam do que não se pode fazer ou calcular.

Por exemplo, é sabido desde os gregos antigos que o número raiz de dois não pode ser escrito como uma fração: isto é, ele não é a razão de dois números inteiros. O mesmo vale para o número pi – a razão entre perímetro e diâmetro da circunferência –, mas isso só foi demonstrado pelo suíço Johann Henirich Lambert (1728 – 1777).

A “formula de Bhaskara”, muito antiga, nos permite resolver equações do segundo grau em uma variável. Há fórmulas mais recentes para resolver equações de terceiro e quarto grau em termos das operações básicas e de raízes ou radicais (quadradas, cúbicas ou de ordem maior). Por muito tempo, tentou-se achar uma fórmula para equações do quinto grau, até que o matemático norueguês Neils Heinrik Abel (1802 – 1829) provou que isto era impossível. O francês Évariste Galois (1811 – 1832) foi mais longe e deu uma receita para descobrir que equações podem ser resolvidas por radicais.

Já no século 20, o austríaco Kurt Gödel (1906 – 1978) mostrou que há afirmações matemáticas verdadeiras, mas impossíveis de se demonstrar. O inglês Alan Turing (1912 – 1954), que inventou a Teoria da Computação a partir dos trabalhos de Gödel, mostrou resultados variados a partir disso: por exemplo, não é possível fazer um programa de computador que funcione como antivírus universal.

Questões de impossibilidade foram e continuam sendo muito importantes para os matemáticos. Em alguns casos, como o de Turing, descobertas deste tipo têm importância prática direta. Em outros, como o de Galois, provar a impossibilidade levou a uma revolução da Matemática pura, que só muito depois desembocou em aplicações (por exemplo, a segurança das compras online são baseadas na Teoria de Grupos que Galois criou). Em todos os casos, quando os matemáticos provam que algo é impossível, isso não é motivo para choro, e sim para se desbravarem novos caminhos.

IV. De volta ao jogo: a ideia de invariante

Como o leitor já percebeu, o jogo dos quadradinhos era apenas um pretexto para falar de impossibilidades. No entanto nosso pequeno drama persiste: como eu posso provar que é impossível preencher todos os quadrados?

A razão é simples. Primeiro, observe que o número total de quadrados no jogo é 15, ímpar. O que mostrarei a seguir é que o número de quadrados marcados ao longo do jogo é sempre par. Desta forma, nunca será possível marcar todos os quadrados.

Para ler o texto na íntegra acesse o site do jornal