Série de reportagens mostra que a Matemática está em tudo

Reprodução do Jornal da USP
Por Denise Casatti – 3º lugar na categoria Matemática do Prêmio Impa-SBM de Jornalismo 2018
Na sala escura, a luz ilumina a mesa do matemático Ton Marar. Estamos no fim da tarde de uma quarta-feira, início de agosto, no primeiro andar do bloco 3 do Instituto de Ciências Matemáticas e de Computação (ICMC) da USP, em São Carlos. Chegamos a um ponto crítico na calmaria morna daquela cena: Marar tenta explicar o que estuda um matemático como ele. Nesse momento, recorda-se de um artigo que escreveu e a lembrança altera de forma drástica o rumo futuro da conversa. Um tornado invade a sala: “Como todos os fenômenos que se manifestam de maneira abrupta, os tornados também podem ser descritos matematicamente”.
A frase emerge do artigo que Marar escreveu para o livro Numa dada situação, lançado durante a 29ª Bienal de São Paulo, em 2010, em conjunto com a obra Tornado, do artista belga Francis Alÿs. Para produzir o vídeo, Alÿs literalmente perseguiu tornados, durante dez anos, fotografando e filmando o fenômeno meteorológico pelo México.
Leia também: Prêmio IMPA-SBM de Jornalismo 2019 abre inscrições
Há 100 anos, eclipse comprovou a Teoria da Relatividade Geral
Hoje comemoramos o acerto de Einstein, mas ele também errou
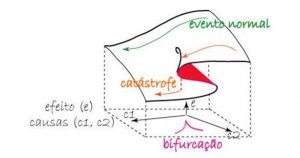
Para explicar matematicamente esse fenômeno, Ton Marar recorre a outro Thom, mais precisamente René Thom, matemático francês que ganhou a famosa Medalha Fields, o Nobel da Matemática, em 1958. Os modelos concebidos por Thom por volta de 1965 deram origem à chamada Teoria da Catástrofe. Para simplificar, pense em processos do tipo causa-efeito como, por exemplo, os ventos que se formam pelo encontro entre massas de ar quente e úmido com massas de ar frio e seco. É comum pensarmos que variações suaves nessas causas também provoquem variações suaves em seus efeitos, certo? “Pois não é bem assim que um tornado nasce”, explica Marar.

Ton Marar chegou ao ICMC aos 17 anos, em 1976, para cursar Bacharelado em Matemática – Foto: Denise Casatti
Se mudarmos continuamente a intensidade das massas de ar, haverá um momento em que os valores atingirão um ponto crítico (ponto de bifurcação) e acontecerá uma transição abrupta no efeito: o vento se tornará um tornado. “Nesse momento ocorre um fenômeno espetacular”, escreve Marar. É quando um vórtice colorido surge, fruto do material que é arrebatado do solo, envolvido por uma nuvem de poeira.
Mas você não precisa estar dentro de um tornado, como Francis Alÿs, para vivenciar a Teoria da Catástrofe. Ela acontece frequentemente, senão todos os dias, no fogão da sua casa, quando você coloca um pouco de água para ferver. No início do processo, na temperatura ambiente, as moléculas que constituem a água estão ligadas por forças de natureza elétrica. Conforme a temperatura aumenta, essas moléculas passam a se movimentar mais rapidamente e essas ligações tornam-se cada vez mais instáveis. Aqui também existe um ponto crítico: o momento em que a temperatura está tão alta e o movimento tão intenso que as moléculas se desconectam e a água passa do estado líquido ao gasoso.
Esse momento singular que acontece no fogão está longe de ser um desastre. É por isso que, para os matemáticos, a Teoria da Catástrofe, apesar do nome, não tem necessariamente a ver com a análise dos fenômenos desastrosos do nosso mundo, mas com o estudo dessas transformações abruptas que estão mais presentes em nosso dia a dia do que podemos imaginar.
Antes que o navio afunde

Durante o minicurso, Isabel mostrou o momento em que o navio vira – Foto: Reinaldo Mizutani
De fato, a máquina de catástrofe que mora no Laboratório de Singularidades do ICMC é totalmente inofensiva: um objeto com o formato de uma parábola, feito de isopor, com alguns pequenos ímãs, incapaz de provocar qualquer fenômeno que se pareça com um tornado. Quando esses ímãs são fixados na superfície desse objeto, seu centro de massa é alterado e a parábola oscila. Se o ímã é colocado em alguns pontos-chave da máquina, ela se torna totalmente instável e tomba. Por isso, ela é chamada de máquina de catástrofe gravitacional.
Os exemplos que Isabel dá estão relacionados a fenômenos que se alteram ao longo do tempo, que pertencem ao campo dos sistemas dinâmicos, uma área que vai ao encontro do jeito de ser de Isabel: extrovertida, falante, sempre gesticulando com os longos cabelos grisalhos encaracolados voando. Até a frase que ela usa para definir o que é uma singularidade tem movimento: “a gota d’água que entorna o balde”.
Há tantas definições possíveis para essa teoria tal como as múltiplas dimensões da realidade que habitam a mente dos pesquisadores dessa área
A agitação de Isabel contrasta com a tranquilidade de David Mond, da Universidade de Warwick, da Inglaterra. Para explicar o que é singularidade, ele recorre à folha de papel e desenha. É um geômetra em ação: constrói três retas que se cruzam em um ponto. “Isso é algo instável”, diz. De volta ao papel, faz as mesmas três retas se cruzarem, mas de outro jeito: no meio, há um espaço entre elas, uma espécie de triângulo irregular, o que faz o cruzamento acontecer em três diferentes pontos. “Isso é estável”, diz. “Uma coisa me interessa muito: descrever como essa coisa instável se torna estável”, acrescenta.
É difícil encontrar uma palavra melhor para descrever Mond do que estabilidade: quando uma nova pergunta é lançada pelo interlocutor, ele faz uma pausa para pensar na resposta mais exata, parece estar calculando cada palavra que usará. “A Teoria de Singularidades está interessada nas formas como os fenômenos instáveis mudam e em descrever todas as diferentes possibilidades de eles se alterarem”, explica. Ele continua, mergulhando no mundo das formas geométricas: “Em matemática, uma coisa acontece frequentemente: alguns objetos que os matemáticos definem têm certos comportamentos complicados. Eles trabalham para entender isso e inventam uma linguagem para descrever essas estruturas. Quando você estuda essas complexas, ricas e complicadas estruturas, você descobre e prova coisas impressionantes, que podem ser aplicadas a outras áreas do conhecimento”.

Damon (à esquerda) e Sotomayor diante da escultura A coisa, uma superfície singular – Foto: Denise Casatti
Aplicar os conhecimentos provenientes da Teoria de Singularidades na área médica é um dos desafios que mobilizam o professor James Damon, da Universidade da Carolina do Norte, nos Estados Unidos. O matemático participa de um grupo multidisciplinar formado por médicos, estatísticos e cientistas da computação que pesquisa imagens médicas relacionadas ao câncer de próstata. “Quando são captadas imagens do seu corpo em 3D, uma das coisas a fazer é identificar precisamente os órgãos e os ossos dentro do seu corpo. Mas essa ainda é uma tarefa muito difícil. Um dos objetivos dos matemáticos é construir modelos de partes do corpo para que possamos identificar precisamente essas estruturas”, conta Damon.
Ele explica que há variações nos modelos e que o desafio dos matemáticos é entender essas variações para poder incorporá-las e encontrar quais modelos melhor se encaixam com a geometria do nosso corpo. “A Teoria de Singularidades é muito útil nessa identificação dos formatos dos objetos e de suas variações”, conta Damon.
A análise de imagens médicas não é o único campo da medicina no qual a Teoria de Singularidades tem muito a contribuir. “Ainda estamos começando a entender como o cérebro humano funciona. Mas os conhecimentos de singularidades combinados com as equações diferenciais possibilitam capturar o comportamento desse sistema”, revela o matemático norte-americano. Ele explica que estudar o cérebro como um todo e analisar seu comportamento é muito mais complexo e desafiador do que pesquisar o funcionamento isolado de suas partes.
Sob diferentes perspectivas
A poucos metros de onde encontramos o matemático Ton Marar, também no primeiro andar do bloco 3 do ICMC, está a sala da primeira mulher a chefiar o Departamento de Matemática do instituto: Maria Aparecida Ruas, ou simplesmente Cidinha, como é carinhosamente conhecida por aqui. Ela é dessas pessoas com quem poderíamos ter uma conversa infinita, se isso fosse possível no plano real. Sua paixão pela matemática transparece na fala delicada, calma e pausada, com a qual é capaz de ensinar, de forma descomplicada, conceitos abstratos e complexos: “Quando você olha para um fenômeno, espera-se que, para ele ser tratado do ponto de vista matemático, você associe a ele equações. Mas sempre que olhamos para uma equação, podemos representar suas soluções no espaço. Então, em vez de olhar apenas para as equações, você também pode olhar para desenhos, para a geometria dos fenômenos”.
Desde que René Descartes criou o sistema de coordenadas, no século 17, os matemáticos estão acostumados a pensar na posição de um ponto (objeto) considerando-se o espaço de duas dimensões (plano). Para localizar esse ponto ou objeto no plano cartesiano, eles se utilizam dos famosos eixos coordenados x e y, dispostos perpendicularmente um ao outro, de forma que a graduação dos eixos se relacionem entre si, indicando o exato lugar do objeto procurado.

Cidinha foi a primeira mulher a se tornar chefe do Departamento de Matemática do ICMC – Foto: Henrique Fontes
Cidinha explica que conseguimos representar um fenômeno no espaço usando duas coordenadas (x e y) se esse fenômeno possuir apenas duas dimensões: largura e altura, por exemplo. Mas se pensarmos em fenômenos com mais do que duas coordenadas (pense em um objeto tridimensional, que tem largura, altura e profundidade), vamos precisar de um espaço de dimensão maior para representá-lo. Por isso, a matemática não se restringe ao mundo tridimensional. “Dependendo do sistema que você analisa, as soluções do seu problema podem estar representadas em uma superfície, em uma curva ou em um objeto maior dentro de um espaço de dimensão maior. Para entender qualitativamente essas soluções, é importante, muitas vezes, entender a geometria dessa representação”, conta Cidinha.
É interessante observar que, até no universo dos matemáticos, há diversas perspectivas sobre as quais podemos analisar um fenômeno: olhando para suas equações, para sua geometria, para as alterações que sofre ao longo do tempo (sistemas dinâmicos), etc. “A Teoria de Singularidades usa ferramentas de diferentes áreas da matemática e as influencia. Isso é muito bonito e unifica a matemática”, acrescenta Isabel. “A riqueza da Teoria de Singularidades vem da sua interação com as diferentes áreas da matemática e também do contato com problemas da ciência e da tecnologia, os quais demandam que os matemáticos os ataquem usando diferentes instrumentos”, completa Jorge Sotomayor, professor aposentado do Instituto de Matemática e Estatística (IME) da USP.
Singularidades em toda parte
Cidinha sempre quis ser professora de matemática. Na lousa da sala, quando ela desenha formas singulares e não singulares, é possível enxergar o gosto que ela tem por ensinar, algo que a habita desde a adolescência. Aos 12 anos, ela já dava aulas particulares de matemática para alunos do ensino fundamental.
“Uma singularidade é uma palavra geral que classifica muitos tipos de comportamentos diferentes do comportamento padrão. Um ponto de bifurcação, por exemplo, indica uma mudança na forma do fenômeno, portanto, indica uma singularidade. Mas nem todo fenômeno singular tem um ponto de bifurcação”, explica. Ela continua: “Uma superfície no espaço, sem singularidades, é suave. Ela não tem quinas, não tem cantos, vértices”. Logo depois, pega um livro nas mãos: “A superfície desse livro tem singularidades ao longo dos pontos de encontro dos lados”, completa. A seguir, faz uma ressalva: “Nem sempre um ponto de encontro é uma singularidade. Se você une duas semirretas e elas viram uma única reta, você não tem singularidade. Mas se você as une de tal forma que formem um ângulo, você já tem um ponto singular”.
Para tornar mais clara a explicação, Cidinha recorre às palavras do matemático japonês Heisuke Hironaka, um dos primeiros a atuar na área da Teoria de Singularidades, laureado em 1970 com a Medalha Fields.
Em uma entrevista publicada em 2005 pela American Mathematical Society, Hironaka diz: “Muitos fenômenos são interessantes, ou algumas vezes desastrosos, porque eles têm singularidades. Uma singularidade pode ser um cruzamento ou alguma coisa que, de repente, muda de direção. Existem muitas coisas assim no mundo, e é por causa disso que o mundo é interessante. De outra forma, o mundo seria completamente plano. Se tudo fosse suave, então, não haveria romances e filmes. O mundo é interessante por causa das singularidades”. O matemático japonês acrescenta ainda: “Sem singularidades, você não pode falar em formas. Quando você faz uma assinatura, se não há cruzamentos, pontas afiadas, é simplesmente um rabisco”.
E você, caro leitor, já analisou sua assinatura? Ela tem cruzamentos? Pontas afiadas? Tem singularidades ou é um simples rabisco? Ao compreender algo sobre a Teoria de Singularidades, ainda que o gesto seja comparável a um leve toque em sua superfície, é possível vislumbrar a beleza que habita o universo sob o ponto de vista dos matemáticos.
Confira aqui as outras reportagens da série.
Leia também: Morre o matemático Vladas Sidoravicius
IMPA abre seleção para analista administrativo


