No Blog de O Globo, a história da epidemiologia matemática
Reprodução
do blog do IMPA Ciência & Matemática, de O Globo, coordenado por Claudio Landim
Ricardo Takahashi — Professor Titular do Instituto de Ciências Exatas, UFMG
Neste momento a epidemia do coronavírus SARS-CoV2, causador da doença chamada Covid-19, vem se propagando pelo planeta e afetando drasticamente a vida das pessoas. Diante de uma situação que a maioria no mundo nunca viu, os governos e a população passam a se perguntar: o que virá pela frente, e o que podemos fazer diante dessa situação? Afinal, entender os padrões segundo os quais os acontecimentos se organizam, recorrer a esse entendimento para imaginar o futuro e para planejar ações que permitam escolher futuros melhores, são parte daquilo que caracteriza a espécie humana. De certa maneira, sentimo-nos desorientados quando as explicações de que dispomos não dão conta de uma realidade à nossa frente.
Diferentemente de outros momentos em que a humanidade já teve de enfrentar outras epidemias e algumas pandemias, em nossa época dispomos de um repertório de conhecimento que nos permite não apenas encontrar explicações para o que está acontecendo mas também tomar decisões que afetam o curso dos acontecimentos, diminuindo os danos, poupando vidas.
Leia também: Congresso das Américas abre inscrições para prêmios
Matemática é aliada para crianças durante quarentena
Por que epidemias crescem exponencialmente? Confira
Uma parte importante do conhecimento que neste momento está sendo utilizado é o da chamada epidemiologia matemática. Essa disciplina foi inaugurada logo após a pandemia da chamada gripe espanhola de 1918-1920, que infectou cerca de um quarto da população mundial, matando dezenas de milhões de pessoas. Assim como a maior parte do conhecimento científico, essa disciplina foi construída a partir das contribuições de inúmeros pesquisadores que foram sendo acumuladas ao longo de décadas, tendo adquirido sua forma a partir do trabalho realizado entre 1927 e 1933 por dois pesquisadores escoceses, Anderson McKendrick e William Kermack.
A teoria de Kermack-McKendrick, como grande parte das teorias científicas mais importantes, é de uma surpreendente simplicidade. Embora seja baseada no conceito de “equações diferenciais” – algo que usualmente só é estudado em cursos superiores da área de ciências exatas – ela é muito fácil de explicar em palavras:
-
Imagine que uma população que esteja passando por uma epidemia seja dividida em três grupos, os susceptíveis (pessoas que não pegaram a doença e podem se infectar), os infectados (pessoas que se encontram doentes) e os recuperados (pessoas que já se curaram, e que portanto têm imunidade ao menos temporária).
-
O número de infectados (I) aumenta, e o número de susceptíveis (S) diminui, à medida em que ocorrem interações entre pessoas do grupo dos infectados e pessoas do grupo dos susceptíveis, pois essa interação leva a que pessoas antes susceptíveis se tornem infectadas.
-
O número de interações entre indivíduos do grupo dos infectados e indivíduos do grupo dos susceptíveis, por sua vez, é proporcional ao número de susceptíveis (S) vezes o número de infectados (I). Por esse motivo, a velocidade da diminuição do número de susceptíveis é proporcional ao produto S × I.
-
O número de infectados, por sua vez, ao mesmo tempo em que sofre um acréscimo quando mais susceptíveis se infectam, sofre também um decréscimo a cada vez que um infectado se recupera. Assim, a velocidade de crescimento do número de infectados é uma soma de dois termos, um proporcional ao produto S × I (ou seja, proporcional ao número de encontros entre infectados e susceptíveis), e o outro significando que a cada momento uma proporção dos infectados irá se curar.
É só isso! As equações que traduzem essa explicação permitem calcular como variam, ao longo do tempo, os números de indivíduos susceptíveis, infectados e recuperados em uma epidemia. Embora nem o leitor nem uma pessoa especializada em matemática sejam capazes de fazer as contas manualmente, uma vez que cada termo muda de valor a cada instante de tempo, hoje em dia é trivial programar um computador para fazer essas contas. Apesar da simplicidade das contas, o resultado é capaz de descrever com precisão vários tipos de epidemias que acontecem no mundo real.
Para se construirem modelos da epidemia da Covid-19, foi verificado que é necessário acrescentar dois grupos adicionais, além dos grupos de susceptíveis, infectados e recuperados: os infectados assintomáticos (pessoas infectadas que não irão desenvolver sintomas) e os expostos (pessoas que se infectaram mas ainda se encontram no período de incubação da doença, antes da manifestação de sintomas). Essa é a base de virtualmente todos os modelos matemáticos que vêm sendo utilizados para estudar a evolução da epidemia da Covid-19.
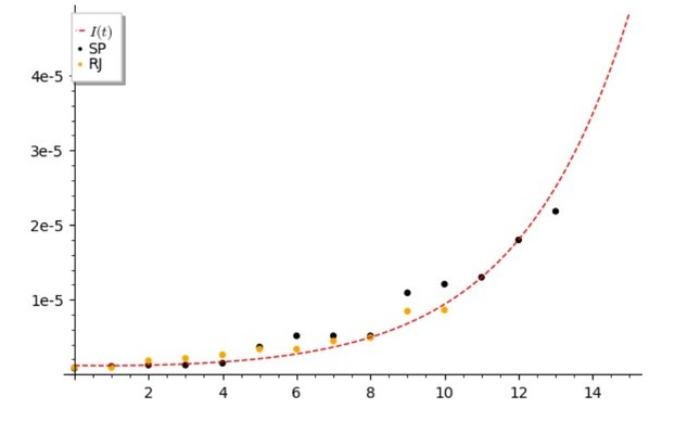
Na figura abaixo, mostro como um modelo desses consegue ajustar o número de casos da Covid-19 nas cidades do Rio de Janeiro e de São Paulo, nas primeiras duas semanas após o início da chamada “transmissão comunitária”.
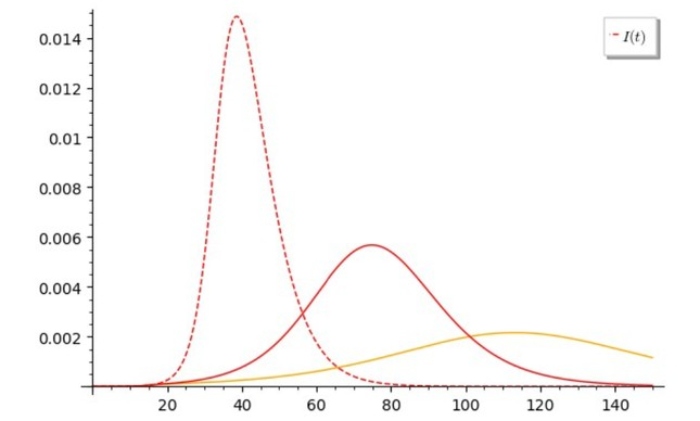
Utilizar um modelo assim, para descrever algo que já aconteceu, é até interessante. Mas o poder de um modelo matemático fica mais evidente quando ele é utilizado para iluminar o que virá pela frente, nos permitindo comparar o que acontece se não fizermos nada com o que pode acontecer se decidirmos fazer algo. O gráfico a seguir ilustra esse ponto, mostrando cenários futuros possíveis.
Em linha tracejada vermelha, o gráfico mostra a evolução ao longo dos dias do número de pessoas infectadas que ocorreria se simplesmente seguíssemos funcionando do mesmo jeito, enquanto esperássemos a epidemia passar. Nesse cenário, haveria um momento em que cerca de 1,5% da população estaria doente ao mesmo tempo, sendo que um quinto desses doentes precisariam de internação hospitalar, representando uma demanda muito acima da capacidade de nosso sistema de saúde. Em São Paulo, isso significaria cerca de 30.000 pessoas precisando de internação simultaneamente.
Mas não precisa ser assim. É possível mudar o comportamento do sistema através do tão falado “isolamento social” que é obtido quando as pessoas ficam em casa ao invés de se movimentarem da maneira usual, assim alterando aquele “número de contatos” que faz parte da equação. Nós, como sociedade, podemos escolher restringir mais ou restringir menos essa frequência dos contatos.
Em linha vermelha contínua é mostrado um cenário em que essas medidas de isolamento social causassem a redução do número de contatos diários entre pessoas para 30% do número usual (reduzindo consequentemente o número de contatos entre infectados e susceptíveis nessa mesma proporção). Nesse cenário, ainda ocorre um momento em que cerca de 0,6% da população está infectada ao mesmo tempo – muito melhor que no caso anterior, mas ainda significando que grande parte daqueles que estiverem doentes durante o pico da epidemia não terão tratamento.
Para ler o texto na íntegra acesse o site do jornal
Leia também: Congresso das Américas abre inscrições para sessões especiais
Furstenberg e Margulis compartilham o Abel Prize 2020